Parallelizing Sorting Algorithms with OpenMP

This blog is originally post on https://blog.sahrohit.com.np/posts/parallel-sorting-algorithm and distributed across platforms for more reach.

This blog focuses on investigating parallel programming using OpenMP, particularly in the context of sorting algorithms. The goal is to compare the performance of serial and parallel implementations of three well-known sorting algorithms—Bubble, Quick Sort, and Merge Sort—on randomly generated numbers, providing insights into how parallel programming impacts computational efficiency.

The blog involves creating both serial (S) and parallel (P) implementations for each of the three sorting algorithms, alongside a reference implementation using STL's std::sort to benchmark the results. The performance of these algorithms is evaluated by measuring the execution times across varying input sizes, and the effects of hyper-threading are also studied.

The hardware setup for the systems used in this blog includes two servers. The first, radish, has 4 cores with 2 threads per core, resulting in 8 virtual CPUs (vCPUs). The second, jalapeno, has 4 cores with 2 threads per core, providing 16 vCPUs, indicating hyper-threading is also enabled. These systems provide a range of hardware configurations for testing the parallel efficiency of sorting algorithms with OpenMP.

Bubble Sort is a simple comparison-based sorting algorithm with quadratic time complexity that works by comparing each item with its adjacent item and swapping to sort. Parallelizing Bubble Sort is challenging due to its inherent sequential nature.

The parallel version of this algorithm alternates between two phases to ensure all elements are correctly positioned. Each thread operates on distinct portions of the data during these phases, improving efficiency by reducing the number of redundant comparisons. The shared state of the array is maintained consistently across threads by using synchronization techniques, such as reduction, to ensure proper sorting without conflicts or race conditions. This approach enables the system to leverage available computational resources fully, speeding up the sorting process, especially for large datasets.

void bubbleSortParallel(int arr[], int n) {
    bool sorted = false;
    int tmp;
    
    while (!sorted) {
        sorted = true;
        
        #pragma omp parallel private(tmp)
        {
            // Even phase
            #pragma omp for reduction(&&:sorted)
            for (int i = 0; i < n-1; i += 2) {
                if (arr[i] > arr[i+1]) {
                    tmp = arr[i];
                    arr[i] = arr[i+1];
                    arr[i+1] = tmp;
                    sorted = false;
                }
            }
            
            // Odd phase
            #pragma omp for reduction(&&:sorted)
            for (int i = 1; i < n-1; i += 2) {
                if (arr[i] > arr[i+1]) {
                    tmp = arr[i];
                    arr[i] = arr[i+1];
                    arr[i+1] = tmp;
                    sorted = false;
                }
            }
        }
    }
}

Quick Sort is a widely used, efficient, and divide-and-conquer algorithm. By recursively partitioning the array, it achieves O(n log n) performance in its average case. Parallelizing Quick Sort is possible by assigning different partitions to different threads.

In the parallel version of Quick Sort, the divide-and-conquer approach is further optimized by assigning different array partitions to separate threads. After partitioning the array around a pivot element, the left and right subarrays are handled independently. This independence allows for parallel execution, where multiple threads can simultaneously sort different parts of the array, greatly reducing the overall sorting time. By controlling the depth of recursion, tasks are conditionally created to avoid excessive parallelization overhead, ensuring that computational resources are utilized efficiently. As a result, parallel Quick Sort can handle large datasets more effectively than its sequential counterpart.

void quickSortParallel(int arr[], int low, int high, int depth = 0) {
    if (low < high) {
        int pi = partition(arr, low, high);

        #pragma omp task shared(arr) if(depth < 3)
        quickSortParallel(arr, low, pi - 1, depth + 1);
        
        #pragma omp task shared(arr) if(depth < 3)
        quickSortParallel(arr, pi + 1, high, depth + 1);
        
        #pragma omp taskwait
    }
}

In the source code, parallelization is achieved through the #pragma omp task directives, which create parallel tasks for sorting the left and right subarrays after partitioning. Specifically, after calculating the pivot index (pi), two separate tasks are spawned: one for sorting the subarray to the left of the pivot (quickSortParallel(arr, low, pi - 1, depth + 1)) and another for the subarray to the right of the pivot (quickSortParallel(arr, pi + 1, high, depth + 1)). These tasks are executed concurrently by different threads.

The condition if(depth < 3) ensures that task creation is limited to the first few recursive levels, which prevents excessive overhead from creating too many tasks in deep recursion. The #pragma omp taskwait directive ensures that the program waits for both sorting tasks to complete before moving forward, maintaining correctness in the overall sorting process. This structured approach efficiently parallelizes the Quick Sort algorithm while balancing task creation and resource usage.

Merge Sort is another divide-and-conquer algorithm with guaranteed O(n log n) performance in the worst case. It is particularly suitable for parallelization since different subarrays can be merged concurrently, making it an ideal candidate for OpenMP.

void mergeSortParallel(int arr[], int l, int r, int depth = 0) {
    if (l < r) {
        int m = l + (r - l) / 2;

        #pragma omp task shared(arr) if(depth < 3)
        mergeSortParallel(arr, l, m, depth + 1);
        
        #pragma omp task shared(arr) if(depth < 3)
        mergeSortParallel(arr, m + 1, r, depth + 1);
        
        #pragma omp taskwait
        merge(arr, l, m, r);
    }
}

In the parallel version of Merge Sort, the array is recursively divided into smaller subarrays that can be sorted independently. The key advantage for parallelization lies in the merging process, where two sorted subarrays can be merged simultaneously in separate threads. This parallel execution of independent subarray sorts significantly reduces the overall runtime, especially for large datasets. The recursion depth is controlled to prevent excessive overhead, ensuring that only the upper levels of recursion are parallelized, where the benefits of parallelism are most significant.

In the source code, parallelization is implemented using the #pragma omp task directive, which creates parallel tasks for sorting the left and right halves of the array (mergeSortParallel(arr, l, m) and mergeSortParallel(arr, m + 1, r)). The if(depth < 3) condition restricts task creation to higher levels of recursion, balancing the trade-off between parallelism and overhead. The #pragma omp taskwait directive ensures that both sorting tasks are completed before proceeding with the merging step, which is crucial for maintaining the correctness of the Merge Sort algorithm.

To evaluate performance, the program generates random arrays of integers, where the size of the arrays was varied from small to large (e.g., 2,500 to 500,000 integers). The random arrays were generated using the command-line arguments for array size and seed value. Each sorting algorithm, both serial and parallel versions (16 threads), was compiled into separate executables, and the execution time was measured.

Each executable took two command-line arguments:

cpp [executable name] [number of random integers to generate] [seed value for random number generation]

Then, a bash script was written to build and execute all the executable and write the runtime of each into a single CSV file.

Parallelization was achieved using OpenMP, with each sorting algorithm being parallelized based on its structure. Execution times were measured using the C++ chrono library, ensuring accuracy. Performance was compared for each algorithm in serial, parallel, and using STL’s std::sort as a reference.

The primary metric used for comparison was execution time in seconds. Tests were performed across a range of input sizes to observe how performance scales with increasing data. The results were plotted in graphs to visualize the difference between serial, parallel, and reference implementations.

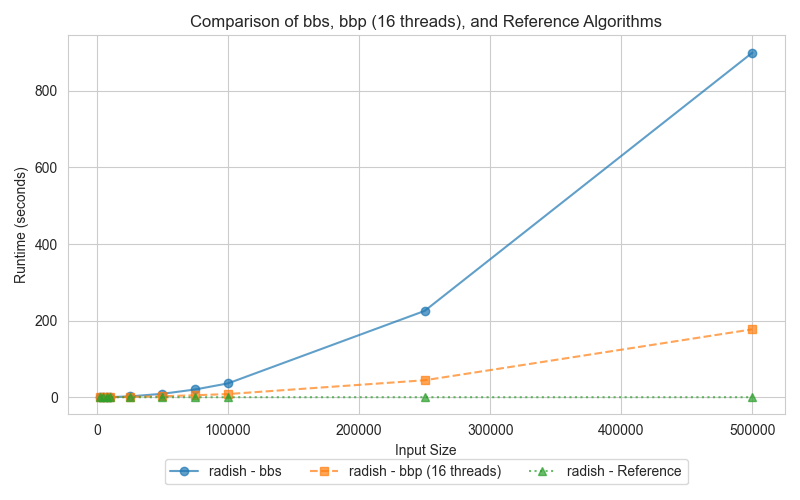
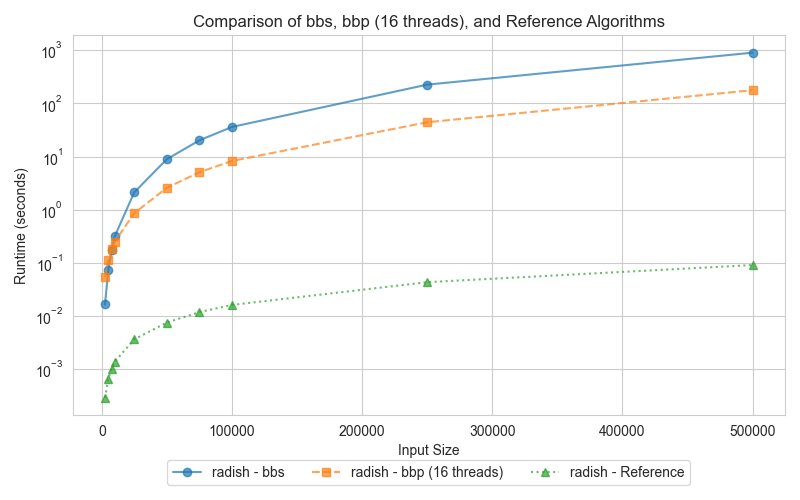
This graph compares the execution times of three sorting implementations: the C++ STL sort, the parallel bubble sort, and the serial bubble sort, for various input sizes. Specifically, the parallel version could be considerably slower for smaller-sized arrays due to the overhead introduced by thread management, synchronization, and cache coherency. However, for larger inputs, its execution time will decrease considerably. This is due to the fact that CPU cores are utilized more effectively, memory access patterns are more efficient, and the hardware prefetching is better exploited, even though both bubble sort implementations have an O(n²) complexity.

For smaller datasets, the overhead associated with managing threads in the parallel version (bbp) leads to slower performance compared to the serial version (bbs). However, as the dataset size increases, the parallel implementation starts to outperform the serial one by distributing the workload across multiple cores. The reference STL sort algorithm consistently surpasses both bbs and bbp due to its sophisticated, optimized design, which includes considerations for memory access patterns, CPU pipelining, and more advanced sorting algorithms with better time complexity.

The weaker performance of parallel bubble sort on smaller arrays stems from the considerable overhead involved in thread creation and synchronization. Additionally, bubble sort’s inherent memory access patterns introduce frequent synchronization barriers due to data dependencies. However, on larger datasets, the increased workload enables parallelism to be more effective, resulting in better performance for bbp compared to its serial counterpart. Nevertheless, both bubble sort variants remain slower than the STL sort, which leverages advanced algorithms and optimizations tailored for modern CPU architectures.

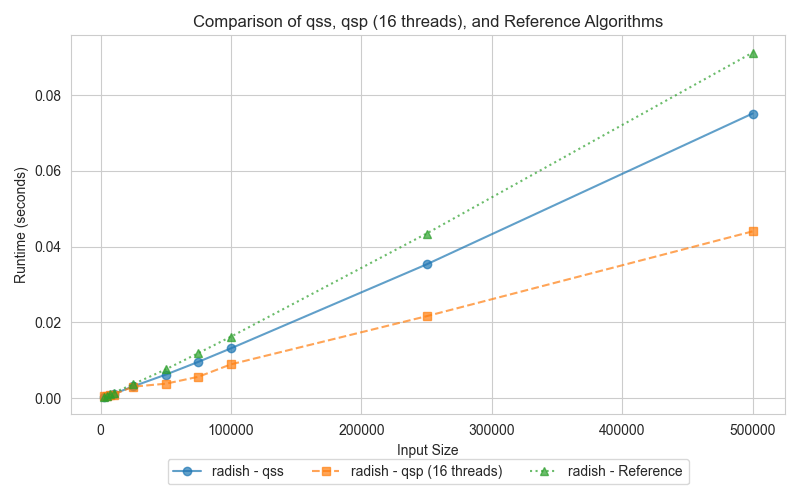
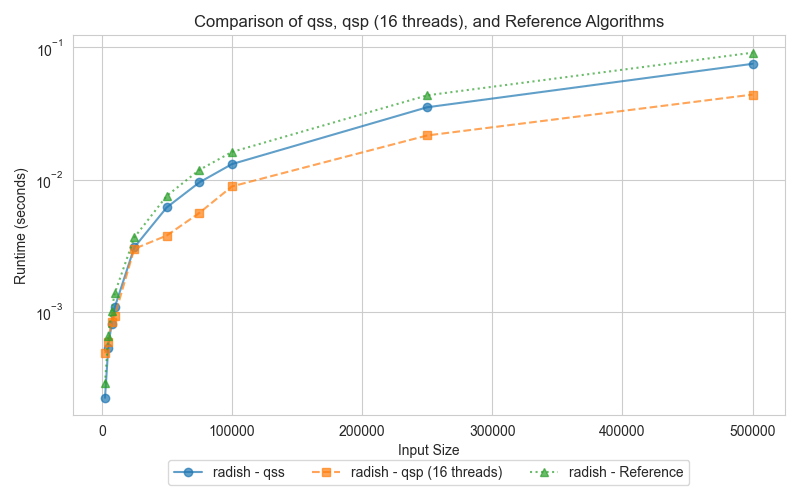
The graphs compare the execution times of three different quick sort implementations: serial (qss), parallel (qsp with 16 threads), and the reference (STL sort). Surprisingly, both the serial and parallel implementations outperform the std::sort, which can be attributed to key differences in the algorithmic approach and optimizations.

For smaller datasets, the serial Quick Sort (qss) performs comparably to the parallel Quick Sort (qsp). As input sizes increase, the parallel version takes advantage of multi-core processing, drastically reducing execution times compared to the serial version. Interestingly, despite the std::sort being highly optimized, both qss and qsp demonstrate faster runtimes. This outcome suggests that the overhead introduced by std::sort's additional optimizations becomes detrimental, especially for the data distributions tested here.

The slower performance of std::sort in this comparison is likely due to the overhead of its more complex optimizations, such as the 3-partition quicksort and the switch to insertion sort for small partitions. While these optimizations are designed for handling worst-case scenarios and duplicate-heavy datasets, they can add unnecessary overhead when such conditions are not present. In contrast, the simpler Lomuto partition scheme used in qss and qsp proves more efficient for the input sizes and data distributions tested here, leading to better performance.

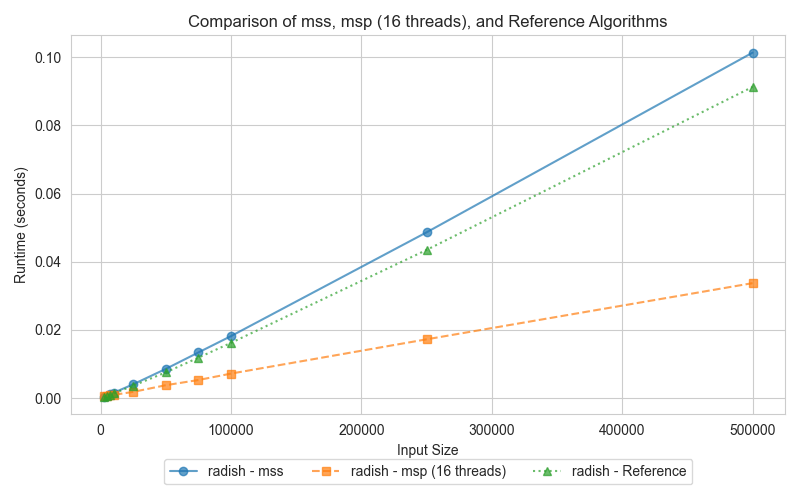
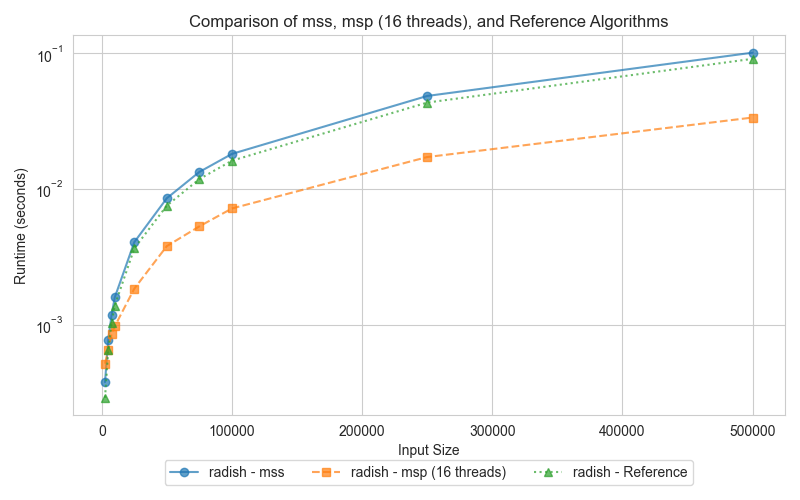
The third graph presents the performance of Merge Sort, comparing the serial version (mss), the parallel version (msp), and the reference (STL sort). Merge Sort is well-suited for parallelization, making it reasonable to expect the parallel version (msp) to outperform the serial counterpart (mss) when tested across dataset sizes. The graph illustrates how the parallel version takes advantage of multi-threading, particularly for larger inputs, while the reference STL sort only performs slightly better than serial merge sort.

The parallel Merge Sort (msp) consistently outperforms the serial version (mss) for larger input sizes. By utilizing 16 threads, msp efficiently splits the array and merges the sections concurrently, significantly improving execution time compared to the serial version (mss). However, for smaller datasets, the overhead of managing multiple threads diminishes msp's advantage. On the other hand, STL sort, while not parallelized, leverages highly efficient algorithms, including a 3-partition quicksort, insertion sort, and heap sort fallback, allowing it to perform slightly better than the serial Merge Sort (mss), particularly on small datasets.

Merge Sort is highly suited for parallelization, as its divide-and-conquer approach naturally allows independent sections of an array to be merged simultaneously. The parallel Merge Sort (msp) significantly reduces execution time for larger datasets by distributing the workload across 16 threads. While the STL sort benefits from optimized memory management and CPU cache utilization, it cannot leverage parallelism, making it slower than msp on large datasets. However, it still manages to outperform the serial Merge Sort (mss) in small data scenarios due to its efficient hybrid algorithms that avoid the worst-case time complexities typical of quicksort.

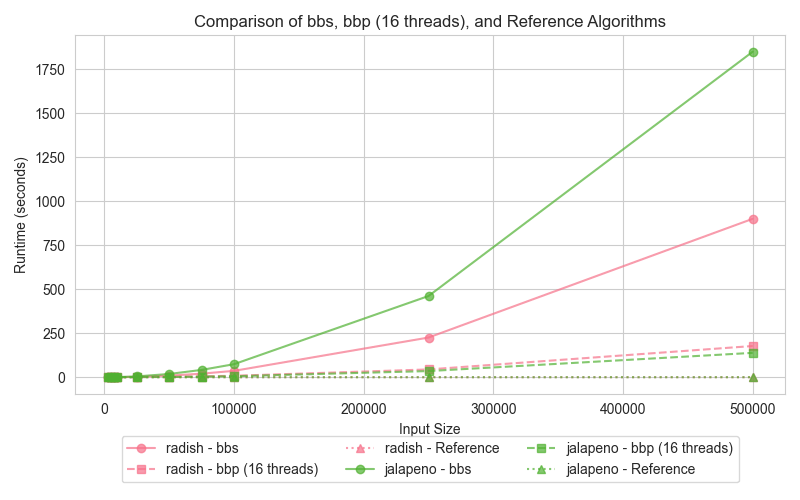
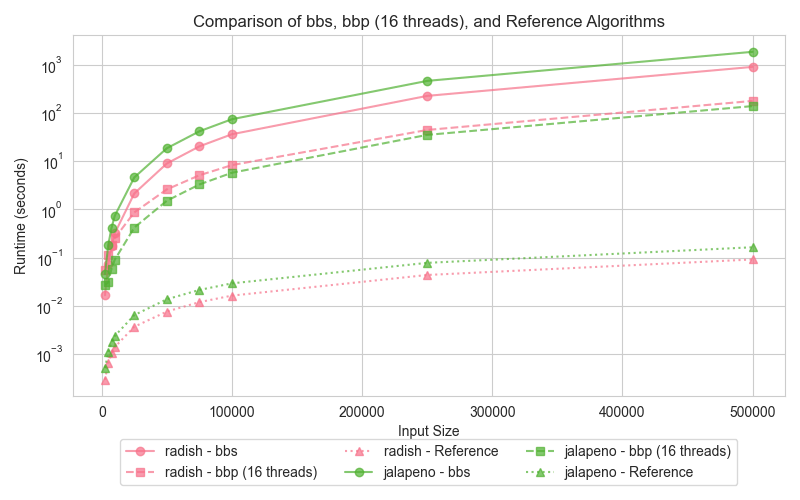
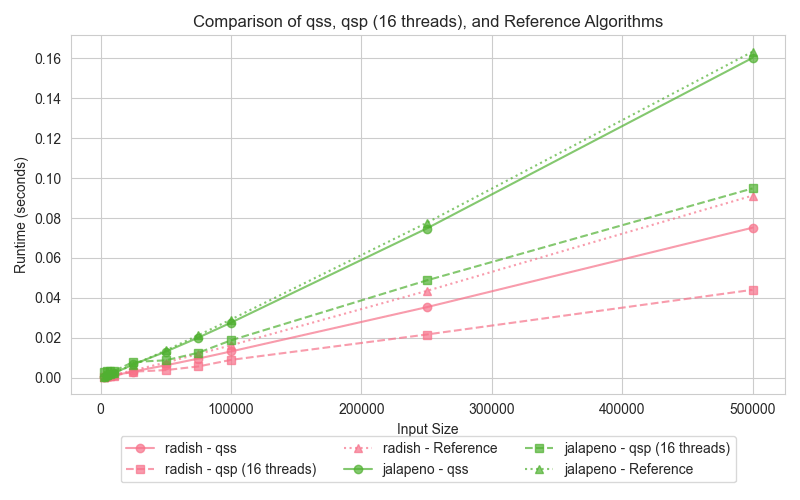
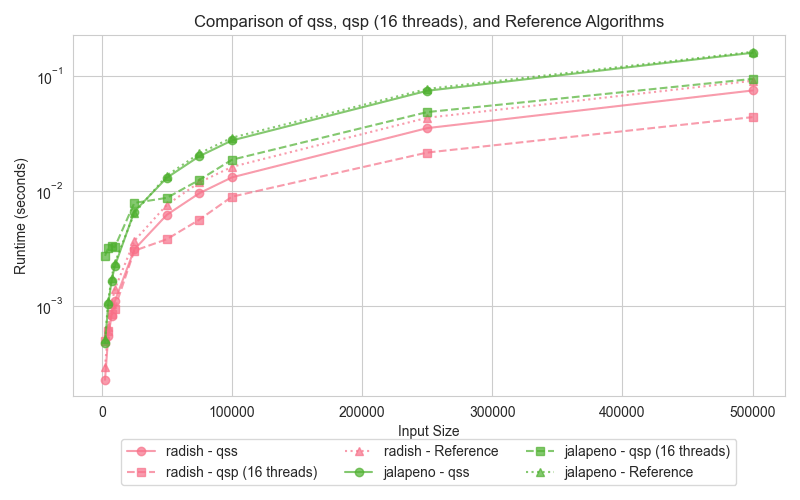
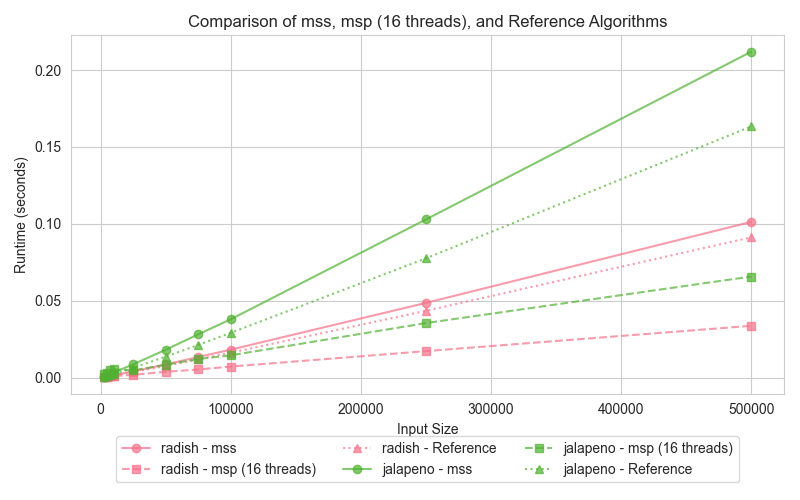
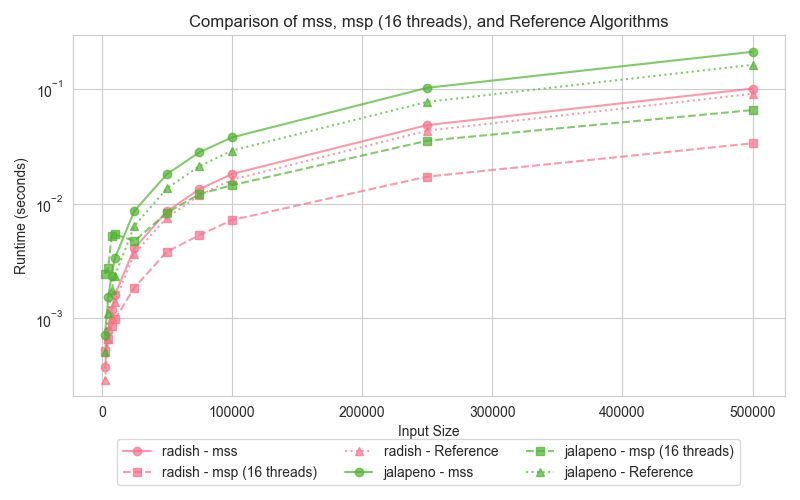
The hyper-threading experiment was conducted on all the above algorithms as the test case. Hyper-threading was enabled and the execution time was measured for varying input sizes. The graph shows the execution times of the hyper threaded runtime decrease in all cases and performs better with hyper-threading.

hyper-threading shows a small improvement in performance for all input sizes, particularly when the workload is large enough to saturate the logical cores. For smaller datasets, hyper-threading introduces minimal benefit as the threads do not fully utilize the available resources.

hyper-threading can provide performance improvements by allowing more threads to run simultaneously, but this is only beneficial when the workload is large enough to keep all logical cores busy. In cases where the workload is too small, the overhead of hyper-threading can actually degrade performance.

The results demonstrate that while parallel implementations of sorting algorithms can provide performance improvements, the benefits are heavily dependent on the size of the dataset and the specific algorithm. For smaller datasets, the overhead of managing threads often negates the benefits of parallelism. However, for larger datasets, parallel versions outperform their serial counterparts. The analysis also shows that hyper-threading can provide performance boosts, but only under certain conditions.

https://github.com/sahrohit/parallel-sorting.git

https://github.com/sahrohit/parallel-sorting/blob/main/combined.csv